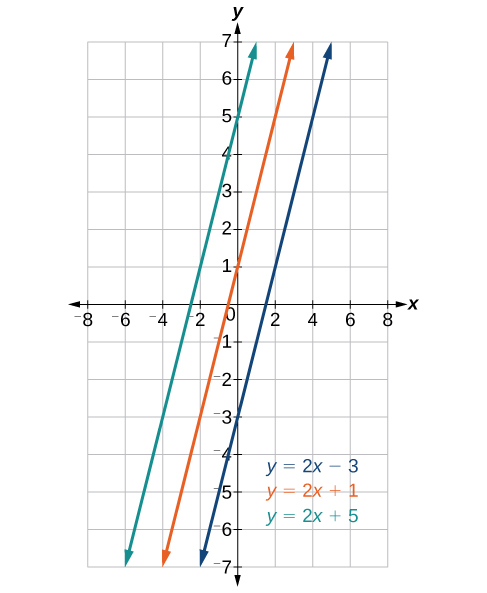
Parallel lines have the same slope and different y-intercepts. Lines that are parallel to each other will never intersect. For example, the figure below shows the graphs of various lines with the same slope, [latex]m=2[/latex].

Parallel lines have slopes that are the same.
All of the lines shown in the graph are parallel because they have the same slope and different y-intercepts. Lines that are perpendicular intersect to form a [latex]^[/latex] angle. The slope of one line is the negative reciprocal of the other. We can show that two lines are perpendicular if the product of the two slopes is [latex]-1:_\cdot _=-1[/latex]. For example, the figure below shows the graph of two perpendicular lines. One line has a slope of 3; the other line has a slope of [latex]-\frac[/latex].
[latex]\begin\text< >_\cdot _=-1\hfill \\ \text< >3\cdot \left(-\frac\right)=-1\hfill \end[/latex]
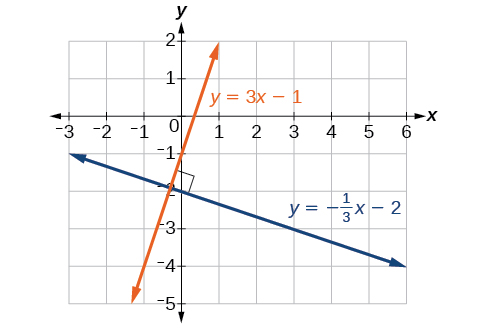
Perpendicular lines have slopes that are negative reciprocals of each other.
Graph the equations of the given lines and state whether they are parallel, perpendicular, or neither: [latex]3y=-4x+3[/latex] and [latex]3x - 4y=8[/latex].
Answer: The first thing we want to do is rewrite the equations so that both equations are in slope-intercept form. First equation:
[latex]\begin3x - 4y=8\hfill \\ -4y=-3x+8\hfill \\ y=\fracx - 2\hfill \end[/latex]

See the graph of both lines in the graph below. From the graph, we can see that the lines appear perpendicular, but we must compare the slopes.
The slopes are negative reciprocals of each other confirming that the lines are perpendicular.
Graph the two lines and determine whether they are parallel, perpendicular, or neither: [latex]2y-x=10[/latex] and [latex]2y=x+4[/latex].

Answer: Parallel lines. Write the equations in slope-intercept form.
Check your work with an online graphing calculator.
We can use a very similar process to write the equation for a line perpendicular to a given line. Instead of using the same slope, however, we use the negative reciprocal of the given slope. Suppose we are given the following line:
The slope of the line is 2 and its negative reciprocal is [latex]-\frac[/latex]. Any function with a slope of [latex]-\frac[/latex] will be perpendicular to [latex]y=2x+4[/latex]. So all of the following lines will be perpendicular to [latex]y=2x+4[/latex].
As before, we can narrow down our choices for a particular perpendicular line if we know that it passes through a given point. Suppose then we want to write the equation of a line that is perpendicular to [latex]y=2x+4[/latex] and passes through the point (4, 0). We already know that the slope is [latex]-\frac[/latex]. Now we can use the point to find the y-intercept by substituting the given values into slope-intercept form and solving for b.
[latex]\beginy=mx+b\hfill & \\ 0=-\frac\left(4\right)+b\hfill & \\ 0=-2+b\hfill \\ 2=b\hfill & \\ b=2\hfill \end[/latex]
The equation for the function with a slope of [latex]-\frac[/latex] and a y-intercept of 2 is [latex]y=-\fracx+2[/latex]. So [latex]y=-\fracx+2[/latex] is perpendicular to [latex]y=2x+4[/latex] and passes through the point (4, 0). Be aware that perpendicular lines may not look obviously perpendicular on a graphing calculator unless we use the square zoom feature.
A horizontal line has a slope of zero and a vertical line has an undefined slope. These two lines are perpendicular, but the product of their slopes is not –1. Doesn’t this fact contradict the definition of perpendicular lines? No. For two perpendicular linear functions, the product of their slopes is –1. As you will learn later, a vertical line is not a function so the definition is not contradicted.
Find the equation of a line perpendicular to [latex]y=3x+3[/latex] that passes through the point (3, 0).
Answer: The original line has slope m = 3, so the slope of the perpendicular line will be its negative reciprocal or [latex]-\frac[/latex]. Using this slope and the given point, we can find the equation for the line.
[latex]\beginy=-\fracx+b\hfill & \\ \text<>0=-\frac\left(3\right)+b\hfill & \\ \text<>1=b\hfill \\ \text< >b=1\hfill \end[/latex]
The line perpendicular to [latex]y=3x+3[/latex] that passes through (3, 0) is [latex]y=-\fracx+1[/latex].
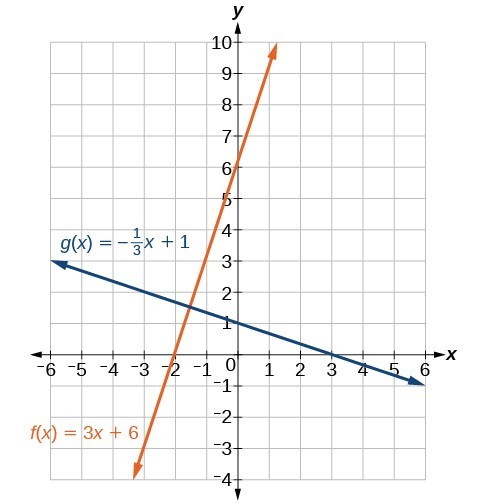
A graph of the two lines is shown below.
Find the equation of the line perpendicular to [latex]5x - 3y+4=0[/latex] which goes through the point [latex]\left(-4,1\right)[/latex].
Answer: The first step is to write the equation in slope-intercept form.
[latex]\begin5x - 3y+4=0\hfill \\ -3y=-5x - 4\hfill \\ y=\fracx+\frac\hfill \end[/latex]
We see that the slope is [latex]m=\frac[/latex]. This means that the slope of the line perpendicular to the given line is the negative reciprocal or [latex]-\frac[/latex]. Next, we use point-slope form with this new slope and the given point.